
El término intervalo procede del latín inter-vallum que quiere decir pausa o espacio. Se catalogan como un subconjunto de los números reales, los cuales pueden ser representando de forma gráfica en una recta numérica a través de una semirecta o de un trazo.
Un intervalo es una serie de números reales que están comprendidos entre dos conjuntos dados: el a y el b, los cuales se conocen como extremos del intervalo.
En pocas palabras es un subconjunto de la recta real que integra un conjunto de números reales.
Los intervalos son representados por medio de una circunferencia vacía o rellena en el extremo.
Otros significados de la palabra intervalo:
- Se llama intervalo a la porción de tiempo o de espacio que hay entre dos hechos o dos cosas, generalmente de la misma naturaleza.
- También es el conjunto de los valores que toma una magnitud entre dos límites dados.Intervalo de temperaturas, de energías, de frecuencias.
- Intervalo es el espacio de tiempo en que quienes han perdido el juicio dan muestras de cordura.
Tipos de intervalos finitos
Se trata de los intervalos de números que corresponden a segmentos de recta.
Intervalo abierto
Se trata del intervalo donde sus extremos no forman parte del conjunto que está representando. En este intervalo se representan todos los números reales que son menores de b y mayores de a.
En estos los valores se separan por una coma y entre paréntesis.
Ejemplo: (a, b)
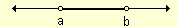
Intervalo cerrado
A diferencia del anterior, en este tipo de intervalo sus extremos siempre forman parte del conjunto al cual representa.
Este intervalo comprende dentro de su extremos a y b, todos los números reales que son iguales o mayores que a, y los iguales o menores que b.
Los valores se representan entre corchetes y separados por una coma. En la imagen prestar especial atención al color de los puntos.
Ejemplo: [a, b]
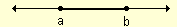
Intervalo semiabierto
También se puede conocer como intervalo semicerrado. Se distingue porque uno de sus lados permanece cerrado mientras que el otro esta abierto, los mismos pueden ser el izquierdo o el derecho.
Los intervalos semiabiertos por la izquierda suelen comprender los números reales iguales o menores que b, y los que son mayores que a. Se representa con la combinación de un corchete cerrado con un paréntesis abierto.
Ejemplo: [a, b)
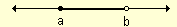
Los intervalos semiabierto por la derecha contienen dentro de sus segmentos números reales menores que b e iguales o mayores que a. Los intervalos se incluyen entre un paréntesis abierto y un corchete cerrado.
Ejemplo: (a, b]
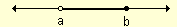
Tipos de Intervalos infinitos
El intervalo infinito se trata de los intervalos que corresponden a la recta real y a la semirecta. En este no se conoce el límite derecho, únicamente visualizándose el límite izquierdo. Los valores en este tipo de intervalos son representados por paréntesis.
Ejemplo: (–¥ , +¥ )

Intervalo infinito abierto a la izquierda
Ejemplo: (a, +¥ )
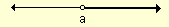
Intervalo infinito cerrado a la izquierda
Ejemplo: [a, +¥ )
En este los intervalos se representan por una corchete abierto y por un paréntesis cerrado.
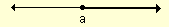
Intervalo infinito abierto a la derecha
Ejemplo: (–¥ , b)
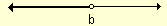
Intervalo infinito cerrado a la derecha
Los intervalos se separan por un coma y se incluye en un paréntesis abierto y un corchete cerrado.
Ejemplo: (–¥ , b]
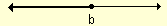
Intervalo negativo
En este tipo de intervalo únicamente se conoce el límite derecho, obviándose por completo el límite izquierdo.
Referencias para este artículo
Especial mención a la Facultad de Ciencias Agrarias (UNL), de donde se han tomado datos y muestras para redactar este artículo.