 Del latín function. La palabra función alude a la correspondencia que existe entre ambos conjuntos. Es la relación que existe entre un conjunto conocido como dominio o X, y un conjunto llamado codominio o Y, donde los elementos del conjunto x le corresponde a un solo elemento del condominio: f (x).
Del latín function. La palabra función alude a la correspondencia que existe entre ambos conjuntos. Es la relación que existe entre un conjunto conocido como dominio o X, y un conjunto llamado codominio o Y, donde los elementos del conjunto x le corresponde a un solo elemento del condominio: f (x).
En pocas palabras, una función es la relación existentes entre dos magnitudes, donde el valor de la primera magnitud le corresponde un solo valor de la segunda.
También se define como función al acto o conjunto de actividades que se realizan siguiendo un orden establecido, en el cual todos los elementos desempeñan un rol y se presentan en un orden para cumplir ciertos objetivos definidos. Es una representación de una obra artística.
En informática se conoce como función aquel subalgoritmo que llega a describir las ordenes en secuencia, donde cada orden tienden una tarea que alude a una población mucho mayor.
Tipos de funciones algebraicas.
 Las funciones algebraicas son aquellas donde aparecen las operaciones de suma, resta, multiplicación, división, potenciación y radicación, Ej.: y=(√3x+5)/(7x³-12). En las funciones algebraicas se deben de realizar las operaciones utilizando varias variables independientes, estas variables son:
Las funciones algebraicas son aquellas donde aparecen las operaciones de suma, resta, multiplicación, división, potenciación y radicación, Ej.: y=(√3x+5)/(7x³-12). En las funciones algebraicas se deben de realizar las operaciones utilizando varias variables independientes, estas variables son:
- División.
- Sustracción.
- Multiplicación.
- Potenciación.
- Adición.
- Radicación.
Clases de funciones algebráicas.
Funciones implícitas: sucede cuando al utilizar una simple sustitución no se logra conseguir las imágenes de X, donde para ello es obligatorio realizar ciertas operaciones. Ejemplo: 5x – y – 2 = 0.
La variable no se halla despejada, es decir, se halla mezclada con la variable x. cuando la regla que define a una función f está dada por una ecuación en x y y, de la forma f(x, y)=0, se dice que la función está dada implícitamente. Ej.: 3x+y-5-2xy=0
Funciones explícitas: son las funciones donde al utilizar una simple sustitución se logra conseguir imágenes de x. Ejemplo: f(x) = 5x – 2.
Es aquella función en donde la variable dependiente y, se halla despejada. Si es posible resolver una ecuación para y en términos de x, se escribe y=f(x) y se dice que la función dada explícitamente. Ej.: y=3x+2.
Funciones polinómicas.
Se trata de todas las funciones que están definidas a través de un polinomio. Estas poseen como dominio un número real que posee imagen (R).
Ejemplo: f(x) = a0 + a1x + a2x² + a2x³ +··· + anxn.
Tipos de funciones polinómicas.
- Funciones cuadráticas: se trata de las funciones polinómicas de segundo grado, las cuales se gráfican con una parábola. Ejemplo: f(x) = ax² + bx + c.
- Funciones constantes: Define aquellas funciones donde su criterio está definido por un número real. En este la recta horizontal se muestra paralela al eje de laS abscisas. Ejemplo: f(x) = k.
- Funciones polinómicas de primer grado: estas funciones se distinguen por su gráfica, la cual se muestra con una recta oblicua que se mantiene definida por medio de dos puntos de la función. Existen varios tipos de estas funciones, como es la función afín, la función lineal y la función de identidad. Ejemplo: f(x) = mx + n.
Funciones racionales.
En estas funciones el criterio llega a ser otorgado por un cociente entre polinomios. Cada uno de los números reales es que forman el dominio excluyendo los valores de x, los cuales llegan a anular el denominador. Función formada por un cociente de polinomios. Estas funciones se pueden representar de la siguiente forma:
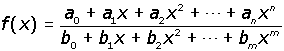
Funciones algebraicas en trozos.
Se refiere aquellas funciones que llegan a ser definidas por criterios variados, donde los intervalos son los únicos que influirán en estos. Existen varios tipos de funciones algebraicas en trozos, como son:
- Funciones signo.
- Funciones en valor absoluto.
- Función mantisa.
- Función parte entera de x.
Funciones radicales.
Tipos de funciones donde el criterio es otorgado por la variable x que se mantiene debajo del signo radical. El dominio cuando la función es irracional y de índice par se creará con aquellos valores que hacen ver el radical igual o mayor que cero. Mientras que el dominio en funciones irracionales con un índice impar siempre será R.
Tipos de funciones trascendentes.

En este tipo de función la variable independiente llega a funcionar como índice de la raíz o como exponente. En ocasiones llega a ser afectada por un signo logarítmico u otro signo que hace uso de la trigonometría. Son las funciones trigonométricas, las trigonométricas inversas, las logarítmicas y las exponenciales.
Existen varios tipos de funciones trascendentes, estos son:
Funciones logarítmicas.
Se trata de aquella función que corresponde a la inversa de la función exponencial en base a. Ejemplo: f(x) = log ª x , a > 0, a ≠ 1.
Funciones trigonométricas.
Función exponencial.
Función que contiene la variable x en el exponente, siendo la base una constante.
Función par.
Función en la que cambiando (x) por (-x) queda la misma expresión.
Ej.: f(x)= f(-x)
Función inversa.
Si f es una función que tiene por dominio al conjunto A y por rango al conjunto B, entonces se llama la función inversa de f, aquella que tiene por dominio el conjunto B y por rango al conjunto A.
Función inyectiva.
También llamada función uno a uno, se caracteriza porque a cada preimagen x є A, le corresponde una y solo una imagen y є B, lo cual se resume en: si X1 ≠ X2, entonces f(X1) ≠ f(X2) para todo X1 y X2 en el dominio.
Existen varios tipos de funciones que son categorizadas como funciones trigonométricas, estas son:
- Función coseno: f(x) = cos x.
- Función cosecante: f(x) = cosec x.
- Función seno: f(x) = sen x.
- Función tangente: f(x) = tg x.
- Función cotangente: f(x) = cotg x.
- Función secante: f(x) = sec x.
Tipos de funciones según la notación f en x, o la expresión algebraica.
Función lineal
Se trata de una función polinómica que se logra distinguir en las gráficas, lo cual siempre resulta una recta. Ejemplo: f(x)= 4x – 2. En esta se obtiene una recta ascendente, donde la pendiente es 4 y el intersecto es 0, -2.
Función constante
Esta función se presenta de la siguiente forma: f(x) = b. En este caso b actúa como una constante. Con estas funciones se logra gráficar una recta horizontal.
Otros tipos de funciones.
- Función creciente. Una función f es creciente sobre un intervalo (rango de dos valores perteneciente a los reales tales que uno es mayor que otro) en R si, para cualquier X1 y X2 en R, donde X1 < X2, se tiene que f(X1) < f(X2), es decir, los valores de función se incrementan.
- Función decreciente. Una función f es decreciente sobre un intervalo en R si, para cualquier X1 y X2 en R, donde X1>X2, se tiene que f(X1) > f(X2), es decir, los valores de función disminuyen.
- Funciones continuas. Es cuando su grafica no presenta ningún corte.
- Funciones discontinuas. Cuando su grafica presenta al menos un corte.
- Función potencial. Función que contiene potencias de la variable x, en donde x se halla elevada a una constante. Ej.: y=[3x+2]³
- Función irracional. Función que contiene raíces. Ej.: y=√3x+2